Oblivious Key-Value Stores and Amplification for Private Set Intersection
不经意键值存储和放大的隐私集合交集
许多最近的隐私集合交集(PSI)协议将输入集编码为多项式。我们考虑更普遍的不经意键值存储(OKVS)的概念,它是一个数据结构,紧凑地表示所需的映射
我们开始了对不经意键值存储的正式研究,并展示了导致迄今为止最快的 OKVS 的新构造。
与布谷鸟散列类似,目前的分析技术不足以找到具体的参数来保证我们的 OKVS 结构的小故障概率。此外,运行实验来验证一个小的故障概率上限的成本太高了。因此,我们展示了新的技术,将一个具有故障概率
最后,我们描述了 OKVS 如何显著改善 PSI 的所有变体的技术水平。这导致了迄今为止最快的两方 PSI 协议,无论是在半诚实还是恶意的情况下。具体来说,在具有中等带宽的网络中(例如,30-300Mbps),我们的恶意双方 PSI 协议的通信量减少了 40%,比以前的最先进的协议快 20-40%,尽管后者只有启发式的信心。
1 介绍
私有集交集(PSI)允许各方了解他们各自持有的集的交集,而不透露关于各个集的其他信息。在几个 PSI 协议(以及密切相关任务的协议)中出现的一种常见技术是将数据编码为多项式。更确切地说,一方插值一个多项式
我们提出了两个主要的贡献。首先,我们抽象了这些应用中需要的多项式的特性,并将 "不经意键值存储"(OKVS)定义为满足这些特性的对象。我们展示了如何构建一个效率更高的 OKVS,它具有线性大小,类似于多项式,并且用高效的线性时间计算取代了多项式插值的任务。第二,我们观察到,目前的分析技术不足以设置具体的参数,以确保我们的 OKVS 构造的失败概率的具体上界(例如
1.1 PSI 的多项式编码
1.2 正确性放大
1.3 我们的成果
2 不经意键值存储
2.1 定义
定义 1. 一个键值存储由一个键集
将一组 键值对作为输入,并输出一个对象 (或者以统计学上的小概率,输出一个错误指标 )。 输入一个对象 ,一个键 ,并输出一个值 。
一个 KVS 是正确的如果对于所有具有不同密钥的
在我们描述的所有算法中,决定
明确地说,人们可以对任何密钥
如果对于所有不同的
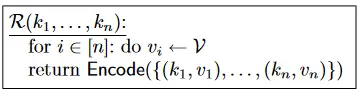
换句话说,如果 OKVS 编码的是随机值(就像在我们的应用中那样),那么对于任何两组密钥
2.2 线性 OKVS
OKVS 的一些应用使用它来编码在某种同态加密原语中处理的数据。在这种情况下,
2.3 二进制 OKVS
一个场
我们一般把注意力限制在
2.4 OKVS 的过拟合
2.5 OKVS 的效率
我们可以根据以下措施来衡量一个 OKVS 的效率。(1) 编码
3 现有的 OKVS 构造
4 新的 OKVS 构造
新的 OKVS 结构旨在改进现有的基于多项式或随机矩阵的 OKVS 结构,其主要问题是改进运行时间,使其与键值对的数量成线性关系。这是以稍微增加 OKVS 的大小为代价的。
5 放大 OKVS 的正确性
6 OKVS 的应用
在这一节中,我们讨论了 OKVS 如何在许多协议中被用作多项式的替代品。
7 其他 PSI 改进
我们提出了对使用 OKVS 的领先 PSI 方案的若干改进。
8 混凝土性能
我们现在对不同的 OKVS 结构和我们的 PSI 方案进行了基准测试。我们还提出了一个基于最先进的半诚实和恶意 PSI 协议的实现的比较。我们使用了半诚实协议(KKRT [23],SpOT-low 和 SpOT-fast [32],CM [7])和恶意协议(RR [40],PaXos [33])的实现,这些协议来自作者提供的开放源代码,并在集合大小
我们假设每对参与者之间有一个经过认证的安全通道(例如,用 TLS)。我们在三种不同的网络设置(所谓的快、中、慢网络)上评估了 PSI 协议。局域网设置(即快速网络)有两台机器在同一地区(弗吉尼亚州),带宽为 4.6 Gib/s;广域网 1(即中等网络)有一台机器在俄亥俄州,另一台在俄勒冈州,带宽为 260 Mib/s;广域网 2(即慢速网络)有一台机器在圣保罗,另一台在悉尼,带宽为 33 Mib/s。虽然我们的协议可以在分组层面上进行并行化,但所有的实验都是用单线程进行的(另有一个线程用于通信)。在本节的所有表格和图表中,"SH" 和 "M" 分别代表半诚实和恶意的意思。我们在完整版中描述了 OKVS 的详细微观基准测试结果。
参考文献
- Ben-Efraim, A., Nissenbaum, O., Omri, E., Paskin-Cherniavsky, A.: PSImple: practical multiparty maliciously-secure private set intersection. ePrint, 2021/122 (2021)
- Botelho, F.C., Pagh, R., Ziviani, N.: Practical perfect hashing in nearly optimal space. Inf. Syst. 38(1), 108–131 (2013)
- Boyle, E., Couteau, G., Gilboa, N., Ishai, Y.: Compressing vector OLE. In: ACM Conference on Computer and Communications Security, pp. 896–912. ACM (2018)
- E. Boyle, G. Couteau, N. Gilboa, Y. Ishai, L. Kohl, and P. Scholl. Efficient pseudorandom correlation generators: Silent OT extension and more. In CRYPTO (3), volume 11694 of LNCS, pages 489–518. Springer, 2019
- Chandran, N., Dasgupta, N., Gupta, D., Obbattu, S.L.B., Sekar, S., Shah, A.: Efficient linear multiparty PSI and extensions to circuit/quorum psi. ePrint 2021/172 (2021)
- Chandran, N., Gupta, D., Shah, A.: Circuit-PSI with linear complexity via relaxed batch OPPRF. Cryptology ePrint Archive, Report 2021/034 (2021)
- Chase, M., Miao, P.: Private set intersection in the internet setting from lightweight oblivious PRF. CRYPTO 2020. Part III, volume 12172 of LNCS, pp. 34–63. Springer, Heidelberg (2020)
- Chen, H., Laine, K., Rindal, P.: Fast private set intersection from homomorphic encryption. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017, pp. 1243–1255. ACM Press, October/November 2017
- Cho, C., Dachman-Soled, D., Jarecki, S.: Efficient concurrent covert computation of string equality and set intersection. In: Sako, K. (ed.) CT-RSA 2016, volume 9610 of LNCS, pp. 164–179. Springer, Heidelberg, Feb. / (2016)
- C. J. Clopper and E. S. Pearson. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika, 26(4), pp. 404–413, 1934
- Dong, C., Chen, L., Wen, Z.: When private set intersection meets big data: an efficient and scalable protocol. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 789–800. ACM Press, November 2013
- Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 1–19. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-54024676-3 1
- Ghosh, S., Nilges, T.: An algebraic approach to maliciously secure private set intersection. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. Part III, volume 11478 of LNCS, pp. 154–185. Springer, Heidelberg (2019)
- S. Ghosh and M. Simkin. The communication complexity of threshold private set intersection. In CRYPTO (2), volume 11693 of LNCS, pages 3–29, 2019
- Graf, T.M., Lemire, D.: XOR filters: faster and smaller than bloom and cuckoo filters. CoRR, abs/1912.08258 (2019)
- Hazay, C., Lindell, Y.: A note on the relation between the definitions of security for semi-honest and malicious adversaries. Cryptology ePrint Archive, Report 2010/551 (2010). http://eprint.iacr.org/2010/551
- C. Hazay and M. Venkitasubramaniam. Scalable multi-party private setintersection. In PKC 2017, Part I, volume 10174 of LNCS, pages 175–203, 2017
- R. Inbar, E. Omri, and B. Pinkas. Efficient scalable multiparty private setintersection via garbled bloom filters. In SCN, pages 235–252, 2018
- Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003)
- Kilian, J.: More general completeness theorems for secure two-party computation. In: 32nd ACM STOC, pp. 316–324. ACM Press, May 2000
- Kirsch, A., Mitzenmacher, M., Wieder, U.: More robust hashing: Cuckoo hashing with a stash. SIAM J. Comput. 39(4), 1543–1561 (2009)
- Kissner, L., Song, D.X.: Privacy-preserving set operations. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 241–257. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218 15
- Kolesnikov, V., Kumaresan, R., Rosulek, M., Trieu, N.: Efficient batched oblivious PRF with applications to private set intersection. In: ACM CCS 2016, pp. 818–829 (2016)
- Kolesnikov, V., Matania, N., Pinkas, B., Rosulek, M., Trieu, N.: Practical multiparty private set intersection from symmetric-key techniques. In: ACM CCS 2017, pp. 1257–1272. ACM Press, October/November 2017
- V. Kolesnikov, M. Rosulek, N. Trieu, and X. Wang. Scalable private set union from symmetric-key techniques. In ASIACRYPT 2019, Part II, volume 11922 of LNCS, pages 636–666. Springer, Heidelberg, 2019
- M. Manulis, B. Pinkas, and B. Poettering. Privacy-preserving group discovery with linear complexity. In ACNS 10, volume 6123 of LNCS, pages 420–437, 2010
- Mitzenmacher, M., Upfal, E.: Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press, Cambridge (2005)
- Moenck, R., Borodin, A.: Fast modular transforms via division. In: Switching and Automata Theory, pp. 90–96 (1972)
- Molloy, M.: The pure literal rule threshold and cores in random hypergraphs. In: SODA, pp. 672–681. SIAM (2004)
- Naor, M., Pinkas, B.: Oblivious transfer and polynomial evaluation. In: 31st ACM STOC, pp. 245–254. ACM Press, May 1999
- Orr` u, M., Orsini, E., Scholl, P.: Actively secure 1-out-of-N OT extension with application to private set intersection. In: Handschuh, H. (ed.) CT-RSA 2017. LNCS, vol. 10159, pp. 381–396. Springer, Heidelberg (2017)
- Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: SpOT-light: Lightweight private set intersection from sparse OT extension. CRYPTO 2019. Part III, volume 11694 of LNCS, pp. 401–431. Springer, Heidelberg (2019)
- Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: PSI from PaXoS: Fast, malicious private set intersection. EUROCRYPT 2020. Part II, volume 12106 of LNCS, pp. 739–767. Springer, Heidelberg (2020)
- Pinkas, B., Schneider, T., Tkachenko, O., Yanai, A.: Efficient circuit-based PSI with linear communication. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. Part III, volume 11478 of LNCS, pp. 122–153. Springer, Heidelberg (2019)
- Pinkas, B., Schneider, T., Zohner, M.: Faster private set intersection based on OT extension. In: Fu, K., Jung, J. (eds.) USENIX Security 2014, pp. 797–812. USENIX Association, August 2014
- Pinkas, B., Schneider, T., Zohner, M.: Scalable private set intersection based on OT extension. ACM Trans. Priv. Secur. 21(2), 7:1–7:35 (2018)
- M. Raab and A. Steger. ”balls into bins” - a simple and tight analysis. In Workshop on Randomization and Approximation Techniques in Computer Science, RANDOM ’98, page 159–170. Springer-Verlag, 1998
- Rindal, P.: Cryptotools. https://github.com/ladnir/cryptoTools
- P. Rindal and M. Rosulek. Improved private set intersection against malicious adversaries. In EUROCRYPT 2017, Part I, volume 10210, pages 235–259, 2017
- Rindal, P., Rosulek, M.: Malicious-secure private set intersection via dual execution. In: ACM CCS 2017, pp. 1229–1242. ACM Press, October/November 2017
- Rindal, P., Schoppmann, P.: VOLE-PSI: fast OPRF and circuit-psi from vector-ole. IACR Cryptol. ePrint Arch. 2021, 266 (2021)
- Schoppmann, P., Gasc ́on, A., Reichert, L., Raykova, M.: Distributed vector-OLE: improved constructions and implementation. In: ACM Conference on Computer and Communications Security, pp. 1055–1072. ACM (2019)
- Walzer, S.: Peeling close to the orientability threshold - spatial coupling in hashingbased data structures. In: Marx, D. (ed.) SODA, pp. 2194–2211. SIAM (2021)
- Zhang, E., Liu, F.-H., Lai, Q., Jin, G., Li, Y.: Efficient multi-party private set intersection against malicious adversaries. In: ACM SIGSAC Conference on Cloud Computing Security Workshop, CCSW 2019, pp. 93–104 (2019)